|
|
|
|
|
|
|
|

Oct 22, 1997Advanced Procedural Texturing Using MMX™ Technology
Dan Goehring and Or Gerlitz
| Information in this document is provided in
connection with Intel products. No license, express or
implied, by estoppel or otherwise, to any intellectual
property rights is granted by this document. Except as
provided in Intel's Terms and Conditions of Sale for such
products, Intel assumes no liability whatsoever, and
Intel disclaims any express or implied warranty, relating
to sale and/or use of Intel products including liability
or warranties relating to fitness for a particular
purpose, merchantability, or infringement of any patent,
copyright or other intellectual property right. Intel
products are not intended for use in medical, life
saving, or life sustaining applications. Intel may make
changes to specifications and product descriptions at any
time, without notice. Copyright (c) Intel Corporation 1997. *Third-party brands and names are the property of their respective owners. |
This application note shows how MMX™ technology-based software procedural texturing can be used for real-time 3D graphics, in the Microsoft* DirectDraw framework. The paper describes how to generate a variety of natural-looking patterns, such as water, stars, grass, wood, and marble, using a mathematical technique called fractional Brownian motion. Procedural texturing requires much less bandwidth than the traditional image-mapping implemented in hardware accelerators.
Two methods for Z-Buffering in the procedural textures are implemented and compared. The Z-Integration technique gives an MMX technology template to be inserted into a scanline algorithm. The second algorithm, while slower, works with all possible scanline rasterizers. The tradeoffs in implementing perspective correction also are discussed.
Performance measurements indicate that an MMX technology optimized complete Z-Buffered perspective-correct marble (worst case) texture requires ~50 clocks per pixel, while a "low-end" marble requires ~37 clocks. Wood takes ~40 clocks, while simple grass takes ~30 clocks. All samples are based on one octave of noise.
2.0 Procedural Texture
Mapping Overview

Photorealistic two- and three-dimensional graphics systems require the ability to apply textures to objects. Textures make objects look more realistic. For example, a room in a 3D game looks more realistic if the walls and floor have interesting patterns, rather than a solid color. Traditional texture mapping methods wrap a 2D bitmap on a 3D object. The procedural texture mapping method produces natural textures on the fly, using mathematical approximations for materials, such as wood, marble, and stone.
Procedural textures are rarely used in real-time, hardware-based rendering engines. Procedural textures use the basic Perlin noise algorithm, which has many variants and is non-standard. In addition, each texture requires a different hardware circuit to implement it, whereas regular texture mapping uses the same circuit, but loads different textures.
For knowledge, procedural textures are rarely used in real-time, software rendering engines, primarily because the calculations are time-consuming. The Perlin gradient noise function interpolates random values that are precomputed for each lattice point in the object space. This computation is floating point intensive and requires many table reads for each texel. In addition, calculations for turbulence and sine wave evaluation make this method even more time-consuming.
These problems seem to imply that the procedural texture method cannot produce the many mega-pixels per sec required for real-time hardware and software engines. However, this application note uses an accelerated MMX technology implementation of Perlin noise to produce fast procedural textures. This method is competitive with regular texture mapping methods.
This application note extends an earlier application note, Using MMX™ Instructions for Procedural Texture Mapping. The original paper highlights the importance of the Perlin noise function. This application note extends the noise function to include fractional Brownian motion (fBm), and wood and marble textures. For each, the application note includes a description of the algorithm and its C and Assembly implementation. The paper also discusses ways to extend the fBm function to create other textures.
The following lists summarizes the strengths and weaknesses of the two different texture mapping methods:
3.0 Fractional Brownian
Motion (Octaves Function)
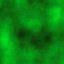
Most procedural texture mapping techniques are based on a NOISE function (e.g. Perlin noise). Generally speaking, noise functions assign each location in space some random value, but in a somehow controllable way. The values are assigned to the integer points and are interpolated for other points. The function can be defined for any dimension (e.g. 1D, 2D, 3D, 4D...) and at arbitrary resolution sampling.
Fractional Brownian motion, by F. Kenton Musgrave, is based on an iterative method which sums different (Perlin) noise values together. To explain how the fBm works, imagine an image like Figure 3.1, treated as a height map. In other words, the colors in the image represent actual heights. Therefore, by looking at the image from the side, an imaginative person might see rolling hills and mountains. Now, repeat this image many times. For each copy of the image, scale the amplitude of the heights of the hills by varying amounts. Next, vary the magnification of the scene for each image. Some scenes might be zoomed out, while other scenes might be zoomed in. Lastly, to form the final image, sum the images together. See Figure 3.2 for an output example.
The number of iterations of Perlin's noise in the fBm are known as "Octaves". Musgrave suggests the number of octaves used should be:
octaves = log_base2(screen.resolution) - 2
For a screen resolution of 640x480,
octaves = log_base2(640) - 2 = ~7 octaves
This is a general rule to follow. Usually, fewer octaves produces an image close to the original and requires less computation time.
 |
 |
| Figure 3.1: Original Perlin noise image. | Figure 3.2: Final fBm output consisting of 7 noise function outputs appropriately scaled and summed together. |
The following diagram shows how the image is built. Seven noise function outputs are scaled and summed together. Noted under each of the images are the zoom factor along with the amplitude modification factor. In practice, experiments show octaves beyond 3 are essentially unneeded.
 +
+  +
+  +
+  +
+  +
+  +
+  =
= 
| Noise #0 | Noise #1 | Noise #2 | Noise #3 | Noise #4 | Noise #5 | Noise #6 | fBm, 7 oct |
| S = 1 | S = 2 | S = 4 | S = 8 | S = 16 | S = 32 | S = 64 | |
| A = 1.000 | A = 0.500 | A = 0.250 | A = 0.125 | A = 0.0625 | A = 0.03125 | A = 0.015625 |
Since the textures in Figures 3.1 and 3.2 are based on fBm, Appendix A shows the code segment used.
The output of fBm can be varied mathematically to form new images. For example, a function can take the output of the fBm function and distorts it in some way to generate wood and marble.
Other textures exist in the book, "Texturing and Modeling, A Procedural Approach", such as:
These textures can be used as 2D textures, or extended into the 3rd dimension. For example, several games on the market use voxel graphics for land generation. fBm can be used to generate height maps for real-time land generation.
While 3D developers have mastered the art of creating indoor scenes, much work is left in adequately depicting the outdoors. Proceduralism can be used to help achieve the effect many are looking for.
4.1 Wood Texturing - Derivation of the Algorithm
 |
| Figure 4.1: Final procedural wood output |
Wood texture can be computed using the relative distance of a point from the tree's axis to construct rings of similar color like wood rings. The algorithm calculates the radius and perturbs it with the turbulence, which is the fractional Brownian motion discussed in Section 3.0. Thus, the wood at point (u,v) is evaluated at (sqrt(u2 + v2) + turbulence(u, v)).
Figure 4.2 is a section of the texture formed from concentric rings that alternate between different shades of brown and black. These rings are modeled by the equation: sqrt(u2 + v2). Each color in Figure 4.2 is an index into an array containing ordered shades of browns. The colors in Figure 4.3 are random offsets in the range of 0 to 63, which were calculated by the fBm using two octaves. These offsets are added to the color indexes in Figure 4.2. The final numerical result is used as an index into an array containing wood colors, which produces the image in Figure 4.4.
 |
+ |  |
= |  |
r = sqrt(u2 + v2) |
The algorithm for wood at texel location x = (u,v) contains four steps:
Wood[] is an array of gradient colors, based on the RenderMan* wood function (The RenderMan Companion: A Programmer's Guide to Realistic Computer Graphics, by Steve Upstill. Published by Addison-Wesley. ISBN 0-201-50868-0). For each point, this wood function uses the fractional part of the perturbed radial distance from the tree axis to build an interpolation scheme between [0-1], going from black to brown in a smooth way. Since MMX™ technology lacks a fast, parallel square root evaluation, step 1 reads the square root values from a table. Another table is used in step 4 for RenderMan's wood function.
The domain of the wood texture is 2D i.e wood = Wood(u,v). If the square root calculation in step 1 is replaced by an absolute value calculation, the final result, after wrapping the 2D wood texture on a 3D object, is almost identical to the original texture. Therefore, step 1 in the algorithm can be replaced by:
All the points (u,v) which obey the equation, |u -v| = c, lie
along the straight line |u - v| - c = 0. This optimization replaces
the serial table reads of the square root values with a fast,
parallel absolute value calculation. The absolute value calculation
takes advantage of the SIMD nature of the MMX instructions.
 |
 |
|
4.2 Wood Texturing
- Code Listing

The following code implements the wood texture algorithm. The SIMD_Octave() procedure pre-calculates the turbulence values and stores them in a buffer. The rest of the algorithm is implemented in the two wood procedures, SIMD_Wood_Linear() and SIMD_Wood_Sqrt().
//*****************************************************************************
// woodPassMMX - calculates turbulence and then calls
// SIMD_Wood_Linear() or SIMD_Wood_Sqrt()
//
// Inputs:
// u_init, v_init: Starting U and V coordinates into the texture map.
// du, dv: Measures the change in U and V for each pixel of the scanline.
// Num_Pix: Length of the scanline in pixels.
// screen_buffer: Pointer to the drawing surface.
// sqrtTable: A pointer to an array containing the square root of 2048 numbers
// woodTable: A pointer to an array containing pre calculated wood colors.
//
//*****************************************************************************
void woodPassMMX(unsigned long u_init, unsigned long v_init,
signed long du , signed long dv,
long Num_Pix , unsigned __int16* screen_buffer)
{
unsigned __int16 alignPixNum;
static unsigned __int16 turbulenceBuf[1024];
unsigned long num_octaves = 3;
//Used for Quad alignment
alignPixNum = (Num_Pix + 3) & 0xFFFFFFFC;
//Clear out the turbulence buffer.
memset(turbulenceBuf, 0, sizeof(__int16) * alignPixNum);
//Calculate the turbulence
SIMD_Octave(u_init, v_init, du, dv, (alignPixNum >> 2), turbulenceBuf, num_octaves);
//Using the averaging scheme for the even pixels while the odd pixels are calculate,
//the first value for pixel #0 isn't truly known. Therefore assign the color of pixel #1
//to pixel #0.
turbulenceBuf[0] = turbulenceBuf[1];
//Calculate the wood colors for the scanline.
if(LINEAR == TRUE)
{
SIMD_Wood_Linear(u_init, v_init, du, dv, alignPixNum);
}
else
{
SIMD_Wood_Sqrt(u_init, v_init, du, dv, alignPixNum);
}
memcpy(screen_buffer, turbulenceBuf, sizeof(__int16) * Num_Pix);
}
Wood Texturing - Table Definitions
The table containing the square root values, sqrtTable, is defined by the following:
for (i = 0; i < 2048; i++) sqrtTable[i] = (unsigned __int16)floor(sqrt((i << 10)));
The Wood table, woodTable, is defined by the following:
This initialization section is used to set up the smooth
gradient wood colors. The colors start off black and smoothly
change to brown.
for (i = 0; i < 6000; i++)
{
//The equation for "r" is just a linear one. If graphed,
//a line with positive slope results. This gives us the backbone
//for the smooth gradients that will be used for the wood color.
r = (float)4.0 * i;
r *= 1.0 / 512.0;
r -= (float)floor(r);
r = smoothstep((float)0, (float)0.83, r) - smoothstep((float)0.83,
(float)1.0, r);
comp_r = 1 - r;
//One r is calculated, the individual red, green, and blue components
//are found. These components are on a scale from 0.0 to 1.0.
wood_red = r * (float)0.30 * 2.0 + comp_r * (float)0.050 * 2.0;
wood_green = r * (float)0.12 * 2.0 + comp_r * (float)0.010 * 2.0;
wood_blue = r * (float)0.03 * 2.0 + comp_r * (float)0.005 * 2.0;
red = ((long)(wood_red * 255)) & 0xF8;
green = ((long)(wood_green * 255)) & 0xFC;
if (FORMAT565)
{
green = ((long)(wood_green * 255)) &; 0xF8;
woodTable[i] = (unsigned __int16)((red << 8) | (green << 3 ) | (blue >> 3));
}
|

|
else
{
green = ((long)(wood_green * 255)) & 0xF8;
woodTable[i] = (unsigned __int16)((red << 7) |
(green << 2 ) | (blue >> 3));
}
}
|

|
For the MMX technology source code listings of SIMD_Octave() and SIMD_Wood(), see Appendix A and Appendix B respectively. For the linear approximation of the sqrt() version of the code, see Appendix G.
5.1 Marble Texturing - Derivation of the Algorithm

Marble has a fractal-like appearance, which can be approximated by evaluating the sine(x + turbulence(x)) and applying a perturbation based on turbulence(x) to the object's normals during the lighting procedure.
The algorithm for marble at location x = (u,v) contains five steps. Steps 1 through 4 are necessary to produce the marble texture. Step 5 is not required, but does improve the overall result by adding lighting.
Figure 5.1 illustrates the first four steps of the marble texture algorithm. The fifth step is part of the lighting procedure and will be explained in Section 7.2.
| Figure 5.1: Result after Step 1 |  |
| Figure 5.2: Intermediate result, u + 10 * turbulence (x) |  |
| Figure 5.3: Result after Step 4 |  |
Since the algorithm uses fixed point arithmetic, the inputs to the sine in step 2 are known in advance. Therefore, the complicated calculation of steps 2, 3 and 4 can be performed in setup time, and stored in a table. During rendering time, the algorithm indexes into this table. Although the reads are serial, they capture only a small amount of time compared to the rest of the parallel computation. The actual marble algorithm at point x = (u,v) is as follows:
The content of the Marble table can be replaced with a different variant every few frames, without impacting overall performance. This saves the overhead of loading a new texture from memory, when using image texture mapping. In addition, the original steps 2, 3 and 4 can be replaced with any texture calculation based on the location ( u ) and the turbulence of (u,v).
 |
 |
 |
 |
 |
| Figure 5.4: One Octave | Figure 5.5: Two Octaves |
Figure 5.6: Three Octaves |
Figure 5.7: Four Octaves |
Figure 5.8: Five Octaves |
When calculating the turbulence, the number of octaves used is critical. As more octaves are used, the computation time increases but the end result is better. See Figures 5.4 to 5.8.
5.2 Marble Texturing - Code Listing
The following code implements the marble texture algorithm. The SIMD_Octave() procedure calculates the turbulence values and stores them in a buffer. The rest of the algorithm is implemented in the SIMD_Marble() procedure. SIMD_Marble() uses the values of the turbulence buffer filled by SIMD_Octave with several octaves of noise. Four pixels are calculated in each iteration.
For the MMX technology source code listings of SIMD_Octave() and SIMD_Marble(), see Appendix A and Appendix C respectively.
//******************************************************************************
//Procedure marblePassMMX()
//
//Inputs:
// u_init, v_init: Starting U and V coordinates into the texture map.
// du, dv: Measures the change in U and V for each pixel of the scanline.
// Num_Pix: Length of the scanline in pixels.
// screen_buffer: Pointer to the drawing surface.
// MarbleTable: A pointer to an array containing the sin of some range of numbers.
//******************************************************************************
void marblePassMMX(unsigned long u_init, unsigned long v_init,
signed long du , signed long dv,
long Num_Pix , unsigned __int16* screen_buffer)
{
unsigned __int16 alignPixNum;
static unsigned __int16 turbulenceBuf[1024];
unsigned long num_octaves = 3;
//Used for Quad alignment
alignPixNum = (Num_Pix + 3) & 0xFFFFFFFC;
//Clear out the turbulence buffer.
memset(turbulenceBuf, 0, sizeof(__int16) * alignPixNum);
//Calculate the turbulence
SIMD_Octave(u_init, v_init, du, dv, (alignPixNum >> 2),
turbulenceBuf, num_octaves);
//Using the averaging scheme for the even pixels while the odd pixels are calculate,
//the first value for pixel #0 isn't truly known. Therefore assign the color of pixel #1
//to pixel #0.
turbulenceBuf[0] = turbulenceBuf[1];
//Calculate the marble colors for the scanline.
SIMD_Marble(u_init, du, alignPixNum);
memcpy(screen_buffer, turbulenceBuf, sizeof(__int16) * Num_Pix);
}
Marble Texturing - Table Definition
During rendering time, the marble table values should be based on the sine(x), where x is a floating point number with a fraction. During initialization, this fraction is approximated by dividing each input by 256. The result is then multiplied by Pi to produce a smooth shape.
The table containing the marble values, marbleTable, is defined by the following.
for (i = 0; i < 5000; i++)
{
val = (double)i / 256.0;
sin_val = (sin(val * Pi) + 1.0) * 0.5;
red = ((long) ((0.33 + 0.66 * sin_val) * 256)) & 0xF8;
blue = ((long) ((0.60 + 0.39 * sin_val) * 256)) & 0xF8;
if (FORMAT565)
{
green = ((long) ((0.27 + 0.72 * sin_val) * 256)) & 0xFC;
MarbleTable[i] = (unsigned __int16)((red << 8) | (green << 3 ) | (blue >> 3));
}
|

|
else
{
green = ((long) ((0.27 + 0.72 * sin_val) * 256)) & 0xF8;
MarbleTable[i] = (unsigned __int16)((red << 7) | (green << 2 ) | (blue >> 3));
}
}
|

|
For the MMX technology source code listings of SIMD_Octave() and SIMD_Marble() see Appendix A and Appendix C respectively.
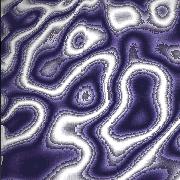
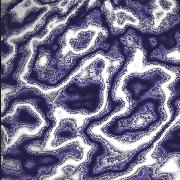
The figures below zoom into the marble texture and demonstrate the difference in the final outcome using 1-5 octaves of Perlin noise.
 |
 |
 |
 |
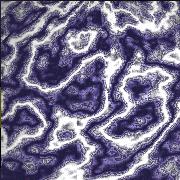 |
| Figure 10.1: One octave |
Figure 10.2: Two octaves |
Figure 10.3: Three octaves |
Figure 10.4: Four octaves |
Figure 10.5: Five octaves |
6.0 Perspective Corrective Dilemmas
With games that use a perspective viewing frustrum instead of an orthogonal view, drawing perspective corrected textures can be difficult. The mathematics required to draw perfect perspective textures is generally too much for a PC to handle real-time. Algorithms can approximate perspective without many viewing artifacts. One algorithm, quadratic approximation, involves finding the per-pixel change in du and dv across each scanline, known as ddu and ddv respectively.
 |
 |
Using ddu and ddv to update du and dv across each scanline poses another problem with the new procedural texture scanline algorithms. The problem is that, since four pixels are calculated in parallel, du, dv, ddu, and ddv must be calculated in parallel, as well. The assembly code needed to set up these parameters is expensive for the CPU to calculate. Therefore as an alternative, the procedural textures developed in this application note do not use ddu and ddv to update du and dv for each pixel drawn.
As a result, if the polygons are too big, gross artifacts develop during the texturing process. There are ways to get around this. One is to keep the polygons small with small scanlines. When only drawing a few pixels, there isn't enough time for errors to accumulate. The other technique is to sub-divide each long scanline into shorter segments. Many short line segments can be put end-to-end to construct a longer segment. For example, if a scanline is 600 pixels long, it can be drawn with 37, 16 pixel scanlines with 8 pixels left over. At the start of each sub-scanline, the du, dv parameters are recalculated to remove error accumulation. This techniques works well but in some instances, a ripple artifact in the textures can be seen. This is because as each pixel is drawn, more errors accumulate. Then after pixel N, the du and dv values are recalculated. Then as more pixels are drawn, the errors begin to accumulate again. At pixel 2N, the du and dv values are recalculated to be exact. With the repetition of this over and over, it can be seen how a ripple develops.
 |
If possible, leave out the DDU and DDV terms. If gross artifacts are noticeable then use the assembly code segment in Appendix D to add the ddu and ddv terms.
The following explains the MMX code in Appendix D. Since four pixels are drawn per loop iteration, four U, V, DU, DV, DDU, and DDV values need to be tracked. Since the even pixels are averaged from the odd pixels then only two U, V, DU, DV, DDU, and DDV terms need to be tracked, for pixels number one and three.
U, V, DU, DV, DDU, and DDV are in 10.22 fixed format. Therefore the code stores the U value for pixels one and three in one register. The V value for pixels one and three is stored in another register. The same is also true for the DU, DV, DDU, and DDV terms.
The following table helps explain the U, DU, and DDU terms for the first sixteen pixels drawn in a scanline.
| Current Pixel | Current U Value | Current DU Value | Current DDU Value |
| Pixel #0: | U | DU | DDU |
| Pixel #1: | U + DU | DU + DDU | DDU |
| Pixel #2: | U + 2DU + DDU | DU + 2DDU | DDU |
| Pixel #3: | U + 3DU + 3DDU | DU + 3DDU | DDU |
| Pixel #4: | U + 4DU + 6DDU | DU + 4DDU | DDU |
| Pixel #5: | U + 5DU + 10DDU | DU + 5DDU | DDU |
| Pixel #6: | U + 6DU + 15DDU | DU + 6DDU | DDU |
| Pixel #7: | U + 7DU + 21DDU | DU + 7DDU | DDU |
| Pixel #8: | U + 8DU + 28DDU | DU + 8DDU | DDU |
| Pixel #9: | U + 9DU + 36DDU | DU + 9DDU | DDU |
| Pixel #10: | U + 10DU + 45DDU | DU + 10DDU | DDU |
| Pixel #11: | U + 11DU + 55DDU | DU + 11DDU | DDU |
| Pixel #12: | U + 12DU + 66DDU | DU + 12DDU | DDU |
| Pixel #13: | U + 13DU + 78DDU | DU + 13DDU | DDU |
| Pixel #14: | U + 14DU + 91DDU | DU + 14DDU | DDU |
| Pixel #15: | U + 15DU + 105DDU | DU + 15DDU | DDU |
For each U update, add the current U value to the previous DU value. For each DU update, add DDU to the previous DU value.
The code calculates only the odd numbered pixels, which are shown in the following table:
| Current Pixel | Current U Value | Current DU Value | Current DDU Value |
| Pixel #1: | U + DU | DU + DDU | DDU |
| Pixel #3: | U + 3DU + 3DDU | DU + 3DDU | DDU |
| Pixel #5: | U + 5DU + 10DDU | DU + 5DDU | DDU |
| Pixel #7: | U + 7DU + 21DDU | DU + 7DDU | DDU |
| Pixel #9: | U + 9DU + 36DDU | DU + 9DDU | DDU |
| Pixel #11: | U + 11DU + 55DDU | DU + 11DDU | DDU |
| Pixel #13: | U + 13DU + 78DDU | DU + 13DDU | DDU |
| Pixel #15: | U + 15DU + 105DDU | DU + 15DDU | DDU |
The initialization code needs to set up U, V, DU, DV, DDU and DDV for pixels one and three. After each loop iteration, U, V, DU, and DV are updated to match the table.
The MMX registers containing the initial U and V values need to be setup as shown below:
;Note: UV values are stored in 10.22 fixed integer format. ;This sets up the U parameters for pixels 1 and 3 in register MM0 and ;V in MM1. After setup, the registers will contain: ; |--------- 32 bit ------------| ; +-------------------------------------------------------------------+ ;MM0 = | U texel for pix #1 = u + du | U texel for pix #3 = u + 3du + 3ddu | ; +-------------------------------------------------------------------+ ; +-------------------------------------------------------------------+ ;MM1 = | V texel for pix #1 = v + dv | V texel for pix #3 = v + 3dv + 3ddv | ; +-------------------------------------------------------------------+
The code in Appendix D shows how this is done.
For the DU and DV initialization, the change in U and V should be measured to see if a pattern develops. Equations can be constructed that model each pattern. Using the formula, DU = U_Next - U_Previous, the following table is developed:
| U Change between Pixel #1 and Pixel #5: | 4DU + 10DDU |
| U Change between Pixel #3 and Pixel #7: | 4DU + 18DDU |
| U Change between Pixel #5 and Pixel #9: | 4DU + 26DDU |
| U Change between Pixel #7 and Pixel #11: | 4DU + 34DDU |
| U Change between Pixel #9 and Pixel #13: | 4DU + 42DDU |
| U Change between Pixel #11 and Pixel #15: | 4DU + 50DDU |
As shown from the above table, the MMX registers used to contain the initial DU and DV values need to be setup as shown below.
;Note: du dv texel values are stored in 10.22 fixed integer format. ;This sets up the du parameters for pixels 1 and 3 in MM0 register and ;dv parameter in MM1 register. After setup, the registers will contain: ; |--------- 32 bit --------------| ; +---------------------------------------------------------------+ ;MM0 = | DU texel for p1 = 4du + 10ddu | DU texel for p3 = 4du + 18ddu | ; +---------------------------------------------------------------+ ; +---------------------------------------------------------------+ ;MM1 = | DV texel for p1 = 4dv + 10ddv | DV texel for p3 = 4dv + 18ddv | ; +---------------------------------------------------------------+
To determine what the DDU and DDV values should be, the change in the DU and DV values is measured when moving from pixel to pixel. Applying the formula DDU = Next DU - Previous DU to the previous table produces the following table of values:
| DU Change between Pixel #1 and Pixel #5: | 16DDU |
| DU Change between Pixel #3 and Pixel #7: | 16DDU |
| DU Change between Pixel #5 and Pixel #9: | 16DDU |
| DU Change between Pixel #7 and Pixel #11: | 16DDU |
| DU Change between Pixel #9 and Pixel #13: | 16DDU |
| DU Change between Pixel #11 and Pixel #15: | 16DDU |
This table shows that the initial values for variables DDU and DDV should be set up in the MMX registers as shown in the following:
;Note: ddu ddv texel values are stored in 10.22 fixed integer format. ;This sets up the ddu parameters for pixels 1 and 3 in MM0 register and ;ddv parameter in MM1 register. After setup, the registers will contain: ; |--------- 32 bit ---------| ; +-----------------------------------------------------+ ;MM0 = | DDU texel for p1 = 16ddu | DDU texel for p3 = 16ddu | ; +-----------------------------------------------------+ ; +-----------------------------------------------------+ ;MM1 = | DDV texel for p1 = 16ddv | DDV texel for p3 = 16ddv | ; +-----------------------------------------------------+
Since the DDU and DDV terms are constant, no additional calculations are required across the scanline.
For each pass through the inner loop, four pixels are drawn and the following variables need to be updated. The MMX register that contains the DU terms needs to be added to the MMX register that contains the U terms. The PADDD instruction needs to be used. The MMX register that contains the DDU terms needs to be added to the MMX register that contains the DU terms. Again the PADDD instruction should be used. The above instructions should also be applied to the V domain.
For a more detailed code listing showing MMX technology instructions please view Appendix D.
7.1 Lighting Tricks - Quick Specular Effect
The classic lighting equation has three components: ambient, diffuse and specular. This equation can be written as:
Color = Ka * Amb_Color + Kd * Obj_Color * (N dot L) + Ks * Light_Color * (R dot V)n
The Gouraud method calculates the color at each vertex of the polygon and interpolates it for each internal pixel. The Phong method calculates the color at each internal pixel by interpolating the normal. Phong shading is an expensive calculation, mainly due to the exponent part. Therefore, most graphic systems implement the Gouraud method, often without the specular part.
A high quality lighting procedure which calculates a color for each internal pixel but eliminates the slow exponent part is:
Color = (Ka + Kds * (N dot L)n) * Texture_Color
Instead of calculating (R dot V)n, the term (Ni dot L)n is evaluated at the vertices of the object and interpolated inside the polygon. This substitution is mathematically incorrect since, if n does not equal 1, ((aN1 + bN2 + cN3) dot L)n does not equal a ((N1 dot L)n) + b((N2 dot L)n) + c((N3 dot L)n). However, the result appears similar to real specular highlights, but is faster to calculate. Still this simplified lighting equation must be evaluated at each pixel, since the Texture _Color term is different for consecutive pixels.
7.2 Using Noise to Perturb Color and Normals
The derivative of a 3D Perlin noise function generates a random vector field, which can be used to perturb the object's normals. This method is known as bump-mapping and is implemented in off-line systems such as Pov-Ray. Bump-mapping calculates DNoise(x,y,z) = (DNx, DNy, DNz) and blends this vector with the object's normal at (x,y,z) to make the surface look bumpy.
Deriving a 3D vector field from a 2D noise function is difficult. However, a 2D noise function still provides enough randomness for special effects. The turbulence calculation, sine evaluation, and color blending in the marble algorithm discussed in Section 5.1 incorporate a lot of randomness, which was used to create two effects. The first one uses the color stored in the Marble table, while the second uses the turbulence.
For the first effect, the 16-bit color, which is the output of the texture procedure, is divided by 512. The result's fraction is multiplied by the interpolated 'specular' component and used in the lighting equation. At pixel P, having Texture_ColorP, the final color is calculated as follows:
For the second effect, the 8-9 bit turbulence value is divided by 64. The result's fraction is multiplied by the interpolated 'specular' component and used in the lighting equation. At pixel P, having turbP, the final color is calculated as follows:
 |
 |
 |
| Figure 6.1: Regular lighted texturing |
Figure 6.2: Lighting effect #1 |
Figure 6.3: Lighting effect #2 |
The above images show what is possible when using noise to perturb color and normals. Figure 6.1 is the normal lighted image. Figures 6.2 and 6.3 show what is possible when using the above techniques.
7.3 Fast Float-to-Long Conversion
Due to the C ANSI standard, when an application converts
a number from floating point to integer, the number is truncated.
On Pentium® and Pentium II processors, this truncation is
expensive because it involves changing the floating point control
word. During the rendering process there are many places where
ftol is called: in the polygon setup part and when converting
the output of the lighting to rgb integer values. To save the
extra cycles wasted on truncation, the fast_ftol
procedure presented here 'rounds to nearest'.
C declaration:
extern signed long fast_ftol(float d)
ASM implementation:
Sometimes objects require usage of a Z-Buffer in
the rendering process. A fixed point 16 bit representation for
Z values enables MMX™ technology to process four data elements
(words) in parallel. Using the 'compare' instruction, instead
of branches, prevents the possible stalls after branch miss prediction
on the Pentium® and Pentium II processors.
For a detailed description of fast software Z-Buffering,
see the application note: 3D Z-Buffer Using MMX Technology.
Unlike a conventional texture mapping engine, as
each new texture is developed and written in assembly, Z-Buffering
becomes a problem. The programmer must incorporate optimized Z-Buffer
code for each procedural texture developed. This is difficult
and tedious to do, but there are two solutions to this problem.
One is to come up with a standard Z-Buffer code template that
can be slapped into the appropriate section of the texture mapping
code. The other is to come up with a separate function callable
by procedural texture mappers.
As with most engineering decisions, tradeoffs are
involved. Integrating the Z-Buffer with each procedural texture
function is clearly the fastest choice but requires more work
from the developer.
8.1 Technique
#1: Z-Buffer Integration
The algorithm used for Z-Buffer integration is based
from the application note 3D Z-Buffer Using MMX Technology.
This algorithm removes the jump/compare per pixel typically needed.
The Z-Buffer integration can be broken up into four
sections. The first is the initialization. The next section draws
four 16 bit pixels at a time to the display. For the scan lines
that are not multiples of four, the third section handles the
initialization of registers that will be used to draw three or
less end pixels. The last section draws these pixels.
Section #1 is the initialization section of the standard
Z-Buffer code template. This part should be included outside of
the main rasterization loop. Code is optimized to compute Z values
for four 16 bit pixels at a time. Two 64 bit MMX registers are
split up to accommodate four 32 bit Z-Buffer values. 16 bits are
used for the integer part while 16 bits are used for the fractional
part. For the Z-Buffer write to the depth surface, a 64 bit write
accommodates four pixels at a time (this is because the 16 bit
fractional part of each Z-value is discarded).
Variable definitions:
"z_start" and "dz" were two variables
given to us in the beginning of the procedure. The following code
segment shows how the variables "high_z", "low_z",
and "z_inc" are calculated.
After initialization, the variables hold the following information:
Once the memory write occurs, this is what the first 8 bytes will look like:
Section #2: After initialization, this section draws pixels in multiples of four.
Section #3: For the three or less pixels at the end
of the scanline, the following code template can be used. This
initializes certain registers and variables therefore shouldn't
be put into the main loop. This part is used to point ESI to the
Z-Buffer where the pixel write is going to occur. CX will contain
the current Z-depth value.
Section #4: This section handles drawing the pixels
and Z-Buffer update for the three or less pixels at the end of
the scanline. This code is based on traditional Z-Buffering. A
compare is made and a branch is taken depending on the results
of the compare. The code is self-explanatory so no explanation
will be given.
Programmer dilemmas:
8.2 Technique
#2: All-purpose Z-Buffer
This routine is simpler to use but less efficient
than technique #1. The Z-Buffer function takes as input the following:
The function then runs through each of the pixels
in the scanline and determines whether or not the pixel should
be drawn based on the calculated Z-values. This allows the programmer
to put any information into the off-screen scanline buffer. Then
the Z-Buffer function writes pixels to the display depending on
the Z-depth values.
The code template below is not optimized and shouldn't
be used in a real application but is provided to help explain
what is going on.
More optimized versions can be written by converting
the above into assembly using aligned 64 bit writes with MMX technology.
See Appendix E for a better full featured Z-Buffer scanline
algorithm, fully optimized for the Pentium and Pentium II
processors.
The table below gives clock cycle information on the various code samples
in this document. These results were obtained through
Intel's VTune
profiler utility.
result dd 0 ;(in the data section)
PUBLIC _fast_ftol
_TEXT SEGMENT
_d$ = 4
_fast_ftol PROC NEAR
fld DWORD PTR _d$[esp]
fistp DWORD PTR result
mov eax , DWORD PTR result
ret 0
_fast_ftol ENDP
_TEXT ENDS

MOVD MM0, z_start
MOVD MM2, dz
PUNPCKLDQ MM0, MM0
PSLLQ MM2, 32
PADDD MM0, MM2
MOVQ low_z, MM0
PUNPCKHDQ MM2, MM2
PSLLD MM2, 1
PADDD MM0, MM2
MOVQ high_z, MM0
PSLLD MM2, 1
MOVQ z_inc, MM2
Note: The following are what the values look like when stored in a register.
|------- 32 bits ------|
+---------------------------------------------+
MM0 = high_z = | z_start + 3dz | z_start + 2dz |
+---------------------------------------------+
|------- 32 bits ------|
+---------------------------------------------+
MM1 = low_z = | z_start + 1dz | z_start |
+---------------------------------------------+
|------- 32 bits ------|
+---------------------------------------------+
MM2 = z_inc = | 4dz | 4dz |
+---------------------------------------------+
|--- 16 bits ---|
+---------------------------------------------------------------+
Z_Buffer = | z_start + 0dz | z_start + 1dz | z_start + 2dz | z_start + 3dz |
+---------------------------------------------------------------+
Address 0 1|2 3|4 5|6 7
PUSH ESI
MOV ESI, z_buffer ;ESI = pointer to four Z values being looked at in Z-Buffer.
;Get the new Z-Buffer values for the four pixels being drawn.
MOVQ MM4, low_z ;Move two rightmost Z-Buffer values into MM4
PSRAD MM4, 16 ;Discard the fractional part of the two Z values
MOVQ MM2, high_z ;Move the leftmost Z-Buffer values into MM2
PSRAD MM2, 16 ;Discard the fractional part of the two Z values
PACKSSDW MM4, MM2 ;Mesh all four Z-Buffer values into one register
;Update the four pixel screen values.
MOVQ MM2, [ESI] ;MM2 = the old Z values currently in the Z-Buffer.
PCMPGTW MM2, MM4 ;Perform a compare between the old and the new Z values.
MOVQ MM3, MM2 ;Save a copy of MM2 register.
PAND MM1, MM2 ;MM1 = Colors of current pixel 4 pixels to be drawn.
PANDN MM3, [EDI] ;[EDI] = Pointer to existing 4 pixels in the screen buffer.
POR MM1, MM3 ;"OR" old and new contents together for the 4 pixel colors.
MOVQ [EDI], MM1 ;Write out the 4 pixels to video memory.
;Update the four Z-Buffer values.
MOVQ MM3, MM2 ;Save a copy of MM2 register.
PAND MM2, MM4
PANDN MM3, [ESI] ;[ESI] = Pointer to existing 4 Z-Buffer values.
POR MM2, MM3 ;"OR" old and new contents together for the 4 Z values.
MOVQ [ESI], MM2 ;Update the Z-Buffer with the 4 new values.
;Update "high_z" components. This is Z = Z + Z_inc
MOVQ MM0, z_inc
PADDD MM0, high_z
MOVQ high_z, MM0 ;Add Delta_Z to the High Z components.
;Update "low_z" components. This is Z = Z + Z_inc
MOVQ MM0, z_inc
PADDD MM0, low_z
MOVQ low_z, MM0 ;Add Delta_Z to the Low Z components.
;Update the Z-Buffer pointer by four pixels.
ADD z_buffer, 8 ;z_buffer pointer is incremented eight bytes (4 pixels).
;Restore ESI
POP ESI
MOVQ MM2, low_z ;We want the starting Z-Buffer value
PSRLD MM2, 16 ;Truncate the 16 bit fractional part.
MOVD ECX, MM2 ;Copy the Z-value to CX
MOV ESI, z_buffer ;ESI points to the Z-Buffer
end_pixels:
CMP CX, [ESI] ;Compare new Z value against old value in Z-Buffer.
JGE skip_pix ;If new Z value is greater than old then skip the pixel write.
MOVD EAX, MM3 ;Move the previous color to eax
MOV [EDI], AX ;Write 16 bit color to video buffer.
MOV [ESI], CX ;Write new Z value to Z-Buffer.
skip_pix:
ADD EDI, 2 ;Increment the pointer to the video buffer.
ADD ESI, 2 ;Increment the pointer to the Z-Buffer.
PSRLQ MM3, 16 ;Shift to the next color.
DEC EDX ;Decrement the end pixel counter.
JNZ end_pixels ;Repeat if there are more pixels to draw.

void z_buffer(unsigned __int16* screen_pointer, unsigned __int16* temp_buffer,
signed __int16* z_pointer, long z_start, long dz,
unsigned long num_pixels)
{
unsigned long index;
for(index = 0 ; index < num_pixels; index++) { if ((z_start >> 16) < *(z_pointer)) { *(z_pointer) = (signed __int16)(z_start >> 16);
*(screen_pointer) = temp_buffer[index];
}
z_pointer++;
screen_pointer++;
z_start += dz;
}
}
| Pentium® Processor with MMX™ Technology Performance Measurements | |||
| Function Name | % Pairing | CPI | Clocks Required to Draw 4 Pixels |
| Perspective Correct Code | 84.21% | 0.83 | 48 Clocks |
| Z-Buffering Integration, Part I | 50.00% | 2.0 | 22 Clocks |
| Z-Buffering Integration, Part II | 92.86% | 1.21 | 34 Clocks |
| Z-Buffering Integration, Part IV | 80.0% | 2.90 | 29 Clocks |
| Pentium® Processor with MMX™ Technology Performance Measurements | ||||||||||||
| Function Name | % Pairing | CPI | Clocks per Pixel for Various Scanline Lengths | |||||||||
| 4 | 10 | 20 | 40 | 60 | 80 | 100 | 140 | 180 | 220 | |||
| SIMD_Octave( ) | 68.80% | 0.72 | 39.50 | 30.30 | 32.10 | 31.18 | 31.04 | 30.71 | 30.62 | 30.51 | 30.46 | 30.42 |
| SIMD_Wood_Linear( ) | 65.35% | 0.72 | 17.00 | 14.20 | 10.80 | 10.03 | 9.77 | 9.64 | 9.56 | 9.47 | 9.42 | 9.39 |
| SIMD_Wood_Sqrt( ) | 61.82% | 0.74 | 21.25 | 19.10 | 14.85 | 14.05 | 13.78 | 13.65 | 13.57 | 13.48 | 13.43 | 13.40 |
| SIMD_Marble( ) | 64.63% | 0.74 | 11.25 | 9.10 | 6.85 | 6.30 | 6.12 | 6.03 | 5.97 | 5.91 | 5.87 | 5.85 |
The procedures/code segments in the first table are meant to be called outside of the main rasterization loop. Therefore only the number of clocks required for one pass are given. These values are the amount of clock cycles required to calculate four pixel values. To find clks/pix, divide by four. Because these routines are called far less than others, memory stalls occur more often. This significantly drives up the clock/pixel ratio.
The second table lists routines located inside the main rasterization loop. Therefore, per-pixel clock cycles are given as a function of the length of a scanline (4, 10, 20, 40, 60, 80, 100, 140, 180, and 220 pixels).
Note, all measurements of a procedure start when first called and until (and including) the "ret" command. Measurement of the SIMD_Octave() function was with one octave of noise.
To figure out the total amount of clocks required for a procedural texture, follow this rule. First, start out by adding in the amount of clocks required for the SIMD_Octave() function. Multiply this by the number of octaves of noise used. Then add in the appropriate clock value for marble, wood, etc... This will give an approximate value of the performance to expect. Adding in Z-Buffering and texture perspective correction will increase the clock count as shown in the first table.
The table below gives clock cycle information for Pentium® II processor, as measured using the PMONSTAT profiler utility.
| Pentium® II Processor Performance Measurements | ||||||||||
| Function Name | Clocks per Pixel for Various Scanline Lengths | |||||||||
| 4 | 10 | 20 | 40 | 60 | 80 | 100 | 140 | 180 | 220 | |
| SIMD_Octave( ) | 37.00 | 32.80 | 31.14 | 30.07 | 30.46 | 30.35 | 30.28 | 30.20 | 30.15 | 30.12 |
| SIMD_Wood_Linear( ) | 15.75 | 11.75 | 10.55 | 9.90 | 9.68 | 9.57 | 9.49 | 9.41 | 9.37 | 9.34 |
| SIMD_Wood_Sqrt( ) | 19.50 | 15.50 | 14.30 | 13.65 | 13.43 | 13.32 | 13.26 | 13.18 | 13.14 | 13.11 |
| SIMD_Marble( ) | 10.50 | 7.50 | 6.50 | 6.00 | 5.83 | 5.75 | 5.70 | 5.64 | 5.61 | 5.59 |
Both this application note and the earlier application note, Using MMX™ Instructions for Procedural Texture Mapping, present a new approach for implementing procedural textures using MMX technology. Using the Perlin noise function as a building block, wood, marble and grass textures were developed. Based on one octave of noise, marble takes 40 clocks, wood takes 44 clocks, while simple grass takes 30 clocks, as measured on the Pentium® II processor. Perspective correction and z-buffering add more cycles.
Procedural texturing is an advanced rendering technique that requires more CPU time to produce a pixel than simpler techniques. Even a fast SIMD implementation of procedural textures may not produce the 30-60 frames per second required by future 3D applications. However, procedural textures have many advantages, such as low memory bandwidth, infinite resolution, and the ability to create many different natural textures based on a single noise function.
To demonstrate a possible usage of the procedural textures presented in this application note, the marble and wood code was integrated into a Mixed Rendering scheme, where a full-screen scene is rendered by two threads. The hardware thread uses a traditional rendering pipeline for the majority of the scene; the software thread renders a high-quality, small object using procedural textures. The outputs of both threads are combined to produce a single frame for the application.
TITLE Modified form of Perlin's Noise Basis function using MMX(TM) technology
;prevent listing of iammx.inc file
.nolist
INCLUDE iammx.inc
.list
.586
.model FLAT
;***********************************************************************
; Data Segment Declarations
;***********************************************************************
;.DATA
DSEG SEGMENT PARA
;KEY for comments
;P0, P1, P# = Pixel number 0, Pixel number 1, Pixel number # respectively.
;Pix = Pixel
;DU = Derivative of the variable U.
;DDU = Derivative of the variable DU.
;Texel = A point in the texture to be mapped onto the screen. Given by U, V.
;Note: Even though the assembly writes four pixel values through each pass of the
;inner loop, only two of the pixels are directly calculated. The other two pixels
;are averaged from neighboring pixels. According to the current scheme,
; |--- 16 bit ---|
; +-----------------------------------------------------------+
; | Pixel #0 | Pixel #1 | Pixel #2 | Pixel #3 |
; +-----------------------------------------------------------+
;Pixels #1 and #3 are directly calculated. Pixel #2 is averaged from Pixel #1 and
;pixel #3. Pixel #0 is averaged from Pixel #1 and the previous pixel before #0.
;
;Also, the programmer realizes that the pixels are labeled from 0, 1, 2, 3 instead
;of 3, 2, 1, 0 as follows the conventional format of Intel Architecture. This was
;an oversite and not realized until it was too late.
;Variables, u, v, du, dv, ddu, ddv each contain parameters for two
;texels. Since u, v, ..., ddv are 64 bit, then each texel parameter is
;32 bit. (32 bit per texel * two texels = 64 bits). This enables us
;to work with two pixels at one time using MMX technology.
ALIGN 8
u QWORD ?
du QWORD ?
ddu QWORD ?
v QWORD ?
dv QWORD ?
ddv QWORD ?
firstU QWORD ?
firstV QWORD ?
;Since the program only calculates odd pixel values, the even pixel values
;must be averaged. Therefore, for each pass through the inner loop, four
;pixels will be drawn. In order to draw the first pixel, the pixel before
;it must be known for the averaging. This pixel color is contained here.
octShift DWORD 0, 0
turbShift DWORD 0, 0
prev_color DWORD 255
;Various masks. Set up to filter out unwanted bits in MMX registers.
ALIGN 8
mask_32_to_15 QWORD 00007FFF00007FFFh
mask_quad_1 QWORD 0001000100010001h
mask_quad_255 QWORD 00FF00FF00FF00FFh
mask_quad_256 QWORD 0100010001000100h
mask_quad_510 QWORD 01FE01FE01FE01FEh
mask_quad_511 QWORD 01FF01FF01FF01FFh
mask_quad_1536 QWORD 0600060006000600h
mask_double_255 QWORD 000000FF000000FFh
mask_double_FFFF QWORD 0000FFFF0000FFFFh
mask_double_65536 QWORD 0001000000010000h
mask_four_255 QWORD 00FF00FF00FF00FFh
DSEG ENDS
;***********************************************************************
; Constant Segment Declarations
;***********************************************************************
.const
;***********************************************************************
; Code Segment Declarations
;***********************************************************************
.code
COMMENT^
void SIMD_Octave(unsigned long u_init, unsigned long v_init,
long du_init, long dv_init, unsigned long Num_Pix,
unsigned _int16* turb_buffer, unsigned long num_octaves);
^
SIMD_Octave PROC NEAR C USES ebx ecx edi esi,
u_init:DWORD, v_init:DWORD, du_init:DWORD, dv_init:DWORD,
num_pixels:DWORD, turb_buffer:DWORD, num_octaves:DWORD
;Initialization
MOVD MM0, u_init
MOVD MM1, v_init
PUNPCKLDQ MM0, MM0 ;U p1 = u, p3 = u
MOVD MM2, du_init
PUNPCKLDQ MM1, MM1 ;V p1 = v, p3 = v
MOVD MM3, dv_init
PADDD MM0, MM2 ;U p1 = u, p3 = u + du
PADDD MM1, MM3 ;V p1 = v, p3 = v + dv
PADDD MM0, MM2 ;U p1 = u, p3 = u + 2du
PADDD MM1, MM3 ;V p1 = v, p3 = v + 2dv
PUNPCKLDQ MM2, MM2
PUNPCKLDQ MM3, MM3
PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du
MOV [turbShift],0 ;turbShift is the octave number 0,1,2,....
XOR ESI,ESI
MOVQ DWORD PTR firstU , MM0
PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv
MOV [octShift],14 ;octshift is (14 - esi (octave number))
PSLLD MM2, 2 ;DU p1 = 4du, p3 = 4du
MOVQ DWORD PTR firstV, MM1
PSLLD MM3, 2 ;DU p1 = 4dv, p3 = 4dv
MOVQ DWORD PTR du, MM2
MOVQ DWORD PTR dv, MM3
start_octave :
MOV EBX, prev_color
MOV EDI, turb_buffer ;EDI will always be pointer to screen buffer
MOV ECX, num_pixels
SUB EDI, 8
;Get the UV parameters in MMX(TM) technology form.
;Note: UV texel values are stored in 10.22 fixed integer format.
;This sets up the U parameters for pixels 1 and 3 in MM0 register and
;V parameter in MM1 register. After setup, the registers will contain:
; |--------- 32 bit ------------|
; +--------------------------------------------------------------+
;MM0 = | U texel for pix #1 = u + du | U texel for pix #3 = u + 3du |
; +--------------------------------------------------------------+
; +--------------------------------------------------------------+
;MM1 = | V texel for pix #1 = v + dv | V texel for pix #3 = v + 3dv |
; +--------------------------------------------------------------+
;This is because the first four pixels drawn on the screen will have the
;U and V texel values of:
;Pixel #0 = u + 0du
;Pixel #1 = u + 1du
;Pixel #2 = u + 2du
;Pixel #3 = u + 3du
;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged.
MOVQ MM0, DWORD PTR firstU
MOVQ MM1, DWORD PTR firstV
MOVQ DWORD PTR u, MM0
MOVQ DWORD PTR v, MM1
start_scan_line:
;First, the program converts the u and v texel coordinates
;from 10.22 format to 8.8 format. 10.22 format is used for
;decimal accuracy but only 16 of the 32 bits are actually used.
;Because the final format will fit in a 16 bit result, u and v
;values are converted from 4, 32 bit packed values
;to 4, 16 bit packed values that will fit in one MMX register. Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM0 = | U texel - p1 | U texel - p3 | V texel - p1 | V texel - p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;u_16bit = u_init >> 14;
;v_16bit = v_init >> 14;
MOVQ MM1, DWORD PTR u
MOVQ MM3, DWORD PTR octShift
MOVQ MM0, DWORD PTR v
PSRLD MM1, MM3 ;Convert from 10.22 to 10.8
MOVQ MM2, DWORD PTR mask_32_to_15 ;Uses 15 instead of 16 because of signed saturation.
PSRLD MM0, MM3 ;Convert from 10.22 to 10.8
PAND MM1, MM2 ;Convert from 10.8 to 7.8 integer format
PAND MM0, MM2 ;Convert from 10.8 to 7.8 integer format
MOVQ MM3, DWORD PTR mask_quad_1
PACKSSDW MM0, MM1 ;Pack the result into one register
;Calculation of the bx0, by0, bx1, by1 values for both pixels. Output:
; |-8 bit-|
; +-----------------------------------------------------------+
;MM2 = | |BX0 p1 | |BX0 p3 | |BY0 p1 | |BY0 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM3 = | |BX1 p1 | |BX1 p3 | |BY1 p1 | |BY1 p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;bx0 = u_16bit >> 8;
;by0 = v_16bit >> 8;
;bx1 = bx0 + 1;
;by1 = by0 + 1;
MOVQ MM1, DWORD PTR u ;Used for incrementing u for next 4 pix.
MOVQ MM2, MM0
PSRLW MM2, 8
PADDD MM1, DWORD PTR du ;Used for incrementing u for next 4 pix.
PADDUSB MM3, MM2 ;mm3 = 0:BX1(1):0:BX1(3):0:BY1(1):0:BY1(3)
;Calculation of the rx0, ry0 values for both pixels. Final output:
; |-8 bit-|
; +-----------------------------------------------------------+
;MM0 = | |RX0 p1 | |RX0 p3 | |RY0 p1 | |RY0 p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;rx0 = u_16bit & 255;
;ry0 = v_16bit & 255;
PSLLW MM0, 8
MOVQ MM4, MM3
MOVQ MM6, DWORD PTR mask_quad_1
PUNPCKHWD MM4, MM2 ;MM4 = 0:BX0(1):0:BX1(1):0:BX0(3):0:BX1(3)
PUNPCKLWD MM3, MM2 ;MM3 = 0:BY0(1):0:BY1(1):0:BY0(3):0:BY1(3)
PMULLW MM4, MM4 ;MM4 = BX0^2(1):BX1^2(1):BX0^2(3):BX1^2(3)
PSRLW MM0, 8 ;MM0 = rx0 and ry0 param for pix 1, 3
;This section includes calculation of b00, b01, b10, b11. Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM4 = | b01 for p1 | b11 for p1 | b01 for p3 | b11 for p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM5 = | b00 for p1 | b10 for p1 | b00 for p3 | b10 for p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;b00 = random1((random1(bx0) + by0));
;b01 = random1((random1(bx0) + by1));
;b10 = random1((random1(bx1) + by0));
;b11 = random1((random1(bx1) + by1));
MOVQ MM2, MM3
PUNPCKLDQ MM3, MM3 ;MM3 = 0:BY0(3):0:BY1(3):0:BY0(3):0:BY1(3)
PUNPCKHDQ MM2, MM2 ;MM2 = 0:BY0(1):0:BY1(1):0:BY0(1):0:BY1(1)
MOVQ MM5, MM4
MOVQ DWORD PTR u, MM1 ;Used for incrementing u for next 4 pix.
PUNPCKLWD MM4, MM4 ;MM4 = BX0^2(3):BX0^2(3):BX1^2(3):BX1^2(3)
PUNPCKHWD MM5, MM5 ;MM5 = BX0^2(1):BX0^2(1):BX1^2(1):BX1^2(1)
PADDW MM4, MM3
PADDW MM5, MM2
;This section calculates g_b00_0, b_b01_0, g_b10_0, g_b11_0 for pix 1 and 3.
;Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM2 = | g_b00_1 p3 | g_b01_1 p3 | g_b10_1 p3 | g_b11_1 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM3 = | g_b00_1 p1 | g_b01_1 p1 | g_b10_1 p1 | g_b11_1 p1 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM4 = | g_b00_0 p3 | g_b01_0 p3 | g_b10_0 p3 | g_b11_0 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM5 = | g_b00_0 p1 | g_b01_0 p1 | g_b10_0 p1 | g_b11_0 p1 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;g_b00_0 = (random2(b00) & 511) - 256;
;g_b01_0 = (random2(b01) & 511) - 256;
;g_b10_0 = (random2(b10) & 511) - 256;
;g_b11_0 = (random2(b11) & 511) - 256;
;g_b00_1 = (random2(b00 + 1) & 511) - 256;
;g_b01_1 = (random2(b01 + 1) & 511) - 256;
;g_b10_1 = (random2(b10 + 1) & 511) - 256;
;g_b11_1 = (random2(b11 + 1) & 511) - 256;
PMULLW MM4, MM4 ;random1
PMULLW MM5, MM5 ;random1
MOVQ MM2, MM6
MOVQ MM3, MM6
PADDUSW MM2, MM4
PMULLW MM2, MM2 ;random2
PADDUSW MM3, MM5
MOVQ MM1, DWORD PTR mask_quad_256
PMULLW MM3, MM3 ;random2
MOVQ MM7, DWORD PTR mask_quad_511
PMULLW MM4, MM4 ;random2
PMULLW MM5, MM5 ;random2
PSRLW MM2, 2
PSRLW MM3, 2
PAND MM2, MM7
PSRLW MM4, 2
PAND MM3, MM7
PSRLW MM5, 2
PAND MM4, MM7
PAND MM5, MM7
PSUBW MM2, MM1 ;MM2 = g_b##_1 for pixel #3
PSUBW MM3, MM1 ;MM3 = g_b##_1 for pixel #1
PSUBW MM4, MM1 ;MM4 = g_b##_0 for pixel #3
PSUBW MM5, MM1 ;MM5 = g_b##_0 for pixel #1
;Take above data for g_b00_0, b_b01_0, g_b10_0, g_b11_0 for pix 1 and 3
;and rearrange the packed values in the MMX registers.
;Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM2 = | g_b00_0 p3 | g_b00_1 p3 | g_b01_0 p3 | g_b01_1 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM3 = | g_b00_0 p1 | g_b00_1 p1 | g_b01_0 p1 | g_b01_1 p1 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM6 = | g_b10_0 p3 | g_b10_1 p3 | g_b11_0 p3 | g_b11_1 p3 |
; +-----------------------------------------------------------+
; +-----------------------------------------------------------+
;MM7 = | g_b10_0 p1 | g_b10_1 p1 | g_b11_0 p1 | g_b11_1 p1 |
; +-----------------------------------------------------------+
MOVQ MM6, MM2
MOVQ MM7, MM3
PUNPCKHWD MM2, MM4 ;MM2 = g_b00_# and g_b01_# for pix #3
PUNPCKLWD MM6, MM4 ;MM6 = g_b10_# and g_b11_# for pix #3
PUNPCKHWD MM3, MM5 ;MM3 = g_b00_# and g_b01_# for pix #1
MOVQ MM4, MM0 ;Preparing for rx1 and ry1 calculation
PUNPCKLWD MM7, MM5 ;MM7 = g_b10_# and g_b11_# for pix #1
;Calculation of the rx1, ry1 values for both pixels. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM4 = | RX1 p1 | RX1 p3 | RY1 p1 | RY1 p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;rx1 = rx0 - 256;
;ry1 = ry0 - 256;
PSUBW MM4, MM1 ;MM4 = rx1 and ry1 parameters
;Setup for the calculation of u1 and u2 for pix #1. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM1 = | RX0 p1 | RY0 p1 | RX0 p1 | RY1 p1 |
; +-----------------------------------------------------------+
MOVQ MM5, MM0
MOVQ MM1, MM4
PSRLD MM5, 16
PSRAD MM1, 16
PSLLQ MM1, 32
PUNPCKHDQ MM1, MM5
PACKSSDW MM1, MM1
PACKSSDW MM5, MM5
PUNPCKLDQ MM1, MM5
;Calculation for U1 and U2 for pixel #1 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM3 = | U1 for pixel #1 | U2 for pixel #1 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;u1 = rx0 * g_b00_0 + ry0 * g_b00_1;
;u2 = rx0 * g_b01_0 + ry1 * g_b01_1;
PMADDWD MM3, MM1 ;43u, MM3 = u1 and u2 for pixel #1
;Setup for the calculation of v1 and v2 for pix #1. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM5 = | RX1 p1 | RY0 p1 | RX1 p1 | RY1 p1 |
; +-----------------------------------------------------------+
MOVQ MM5, MM4
PSRAD MM5, 16
MOVQ MM1, MM0
PSRLD MM1, 16
PSLLQ MM1, 32
PUNPCKHDQ MM1, MM5
PACKSSDW MM1, MM1
PACKSSDW MM5, MM5
PUNPCKLDQ MM5, MM1
;Calculation for V1 and V2 for pixel #1 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM7 = | V1 for pixel #1 | V2 for pixel #1 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;v1 = rx1 * g_b00_0 + ry0 * g_b00_1;
;v2 = rx1 * g_b01_0 + ry1 * g_b01_1;
PMADDWD MM7, MM5 ;MM7 = v1 and v2 for pixel #1
;Setup for the calculation of u1 and u2 for pix #3. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM1 = | RX0 p3 | RY0 p3 | RX0 p3 | RY1 p3 |
; +-----------------------------------------------------------+
MOVQ MM5, MM0
PSLLD MM5, 16
PSRLD MM5, 16
MOVQ MM1, MM4
PSLLD MM1, 16
PSRAD MM1, 16
PUNPCKLDQ MM1, MM1
PUNPCKHDQ MM1, MM5
PACKSSDW MM1, MM1
PACKSSDW MM5, MM5
PUNPCKLDQ MM1, MM5
;Calculation for U1 and U2 for pixel #3 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM2 = | U1 for pixel #3 | U2 for pixel #3 |
; +-----------------------------------------------------+
PMADDWD MM2, MM1 ;MM2 = u1 and u2 for pixel #3
;Setup for the calculation of v1 and v2 for pix #3. Final output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM4 = | RX1 p3 | RY0 p3 | RX1 p3 | RY1 p3 |
; +-----------------------------------------------------------+
PSLLD MM4, 16
PSRAD MM4, 16
MOVQ MM5, MM0
PSLLD MM5, 16
PSRAD MM5, 16
PUNPCKLDQ MM5, MM5
PUNPCKHDQ MM5, MM4
PACKSSDW MM5, MM5
PACKSSDW MM4, MM4
PUNPCKLDQ MM4, MM5
;Calculation for V1 and V2 for pixel #3 -> After multiplication... Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM6 = | V1 for pixel #3 | V2 for pixel #3 |
; +-----------------------------------------------------+
PMADDWD MM6, MM4 ;MM6 = v1 and v2 for pixel #2
;Calculation for SX and SY for pixels #1 and #3, Output:
; |--- 16 bit ---|
; +-----------------------------------------------------------+
;MM1 = | SX p1 | SX p3 | SY p1 | SY p3 |
; +-----------------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;sx = (((rx0 * rx0) >> 1) * ((1536 - (rx0 << 2))))>> 16;
;sy = (((ry0 * ry0) >> 1) * ((1536 - (ry0 << 2))))>> 16;
MOVQ MM5, MM0
PMULLW MM5, MM5
MOVQ MM4, MM0
MOVQ MM1, DWORD PTR mask_quad_1536
PSLLW MM4, 2
PSUBD MM6, MM2 ;V1 - U1 and V2 - U2 for P3
PSUBD MM7, MM3 ;V1 - U1 and V2 - U2 for P1
PSUBW MM1, MM4
PSRLW MM5, 1
PMULHW MM1, MM5 ;MM1 = sx and sy param for pix 1, 3
;Calculation of A and B for pixel #1 and #3. Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM7 = | A for pixel #1 | B for pixel #1 |
; +-----------------------------------------------------+
; +-----------------------------------------------------+
;MM6 = | A for pixel #3 | B for pixel #3 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;a = u1 + sx * ((v1 - u1) >> 8);
;b = u2 + sx * ((v2 - u2) >> 8);
PSRAD MM7, 8
PSRAD MM6, 8
MOVQ MM4, MM1
MOVQ MM5, MM1
PSRLQ MM4, 16
PUNPCKLWD MM1, MM1
PUNPCKHDQ MM4, MM4
PMADDWD MM7, MM4
PSLLD MM5, 16
MOVQ MM4, DWORD PTR v ;Used for incrementing v for next 4 pix
PSRLD MM5, 16
PUNPCKHDQ MM5, MM5
PADDD MM4, DWORD PTR dv ;Used for incrementing v for next 4 pix
PADDD MM7, MM3 ;MM7 = a and b parameter for pix #1
PMADDWD MM6, MM5
MOVQ MM3, DWORD PTR mask_double_65536
PSRLD MM1, 16
MOVQ DWORD PTR v, MM4 ;Used for incrementing v for next 4 pix
;Calculation of color indexes for pixel #1 and #3. Output:
; |--------- 32 bit ---------|
; +-----------------------------------------------------+
;MM7 = | Color index for pixel #1 | Color index for pixel #3 |
; +-----------------------------------------------------+
;This code correlates to the following "C" code in the "C_Noise()" function.
;color = (a + 65536 + sy * ((b - a) >> 8)) >> 9;
PADDD MM6, MM2 ;MM6 = a and b parameter for pix #3
MOVQ MM4, DWORD PTR mask_quad_510
MOVQ MM2, MM6
PUNPCKLDQ MM6, MM7
MOVD MM0, ebx ;Move the last color written into MM2
PUNPCKHDQ MM2, MM7
PADDD MM3, MM2
PSUBD MM6, MM2
PSRAD MM6, 8
PMADDWD MM6, MM1
PADDD MM6, MM3
PSRLD MM6, 9 ;MM6 = color for pix #1 and #3
;Since the color values have been calculated for pixels 1 and 3,
;pixels 0 and 2 still need to be determined. Pixel 0 is calculated by
;(prev_pixel + pixel #1) / 2 and pixel 2 is calculated by (pixel #1 +
;pixel #3) / 2. Output:
; |--- 16 bit ----|
; +-----------------------------------------------------------------+
;MM3 = |Color p0 index | Color p1 index | Color p2 index | Color p3 index|
; +-----------------------------------------------------------------+
MOVD MM4, DWORD PTR mask_double_255
PACKSSDW MM6, MM6
MOVQ MM7, MM6
MOVQ MM3, MM6
PSRLD MM7, 16
PUNPCKLWD MM7, MM0
PADDW MM6, MM7
PSRLW MM6, 1
PUNPCKLWD MM3, MM6
ADD EDI, 8
;Now that MM3 contains the 4 memory indexes in packed format, we need
;to unpack them in order to get the precomputed color values from the 256
;element color array. Output:
; |--- 16 bit ---|
; +--------------------------------------------------------------+
;MM1 = | Color p3 | Color p2 | Color p1 | Color p0 |
; +--------------------------------------------------------------+
;Write the 4 pixel colors to the backbuffer.
;Decrease the counter and loop back to draw four more pixels if necessary.
;The looping construct may look strange but it is done to allow for the
;calculation of the pixel colors at the end of the scan line.
;Or : divide(right shift) by the octave index and add to the prev ones
MOVD EBX ,MM3
PSRLW MM3,[turbShift]
PADDW MM3,[EDI]
MOVQ [EDI], MM3 ;Write out the 4 pix to video memory.
DEC ECX
JNZ start_scan_line
INC ESI
INC [turbShift]
DEC [octShift]
CMP ESI, num_octaves
JNZ start_octave
MOV prev_color, EBX ;EBX is the color index of pixel #3. Store it.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; here we rearrange the turb buffer
;; buffer[i] = p0:p1:p2:p3 --> buffer[i] = p3:p2:p1:p0
MOV EDI, turb_buffer
MOV ECX, num_pixels
flipLoop:
MOVQ MM5, [EDI]
MOVQ MM4, MM5
PUNPCKHDQ MM5, MM5 ;MM5 = p0:p1:p0:p1
MOVQ MM7, MM5 ;MM7 = p0:p1:p0:p1
PSRLD MM5, 16
MOVQ MM6, MM4
PUNPCKLWD MM5, MM7 ;MM5 = *:*:p1:p0
PSRLQ MM6, 16 ;MM6 = 0:p0:p1:p2
PUNPCKLWD MM6, MM4 ;MM6 = *:*:p3:p2
PUNPCKLDQ MM5, MM6 ;MM5 = p3:p2:p1:p0
MOVQ [EDI], MM5
ADD EDI, 8
DEC ECX
JNZ flipLoop
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
EMMS ;Clear out the MMX registers and set appropriate flags.
RET ;End of function
SIMD_Octave ENDP
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
END
Appendix B - Wood (Sqrt) Code Listing
TITLE wood textures using MMX(TM) technology
;prevent listing of iammx.inc file
.nolist
INCLUDE iammx.inc
.list
.586
.model FLAT
KLAM equ 0
;***********************************************************************
; Data Segment Declarations
;***********************************************************************
;.DATA
DSEG SEGMENT PARA
extrn _marbleTable : ptr sword
extrn _woodTable : ptr sword
extrn _sqrtTable : ptr sword
extrn _turbulenceBuf : ptr sword
;Variables, u, v, du, dv each contain parameters for two
;texels. Since u, v, ... are 64 bit, then each texel parameter is
;32 bit. (32 bit per texel * two texels = 64 bits). This enables us
;to work with two pixels at one time using MMX technology.
ALIGN 8
_4du QWORD ?
_4dv QWORD ?
result dd 0
;Various masks. Set up to filter out unwanted bits in MMX registers.
ALIGN 8
const_quad_10 QWORD 000a000a000a000ah
const_quad_15 QWORD 000f000f000f000fh
const_FFFF_Minus_High_sqrt QWORD 0f800f800f800f800h
const_FFFF_Minus_High_Wood QWORD 0e890e890e890e890h
mask_odd_indexes QWORD 0fffefffefffefffeh
mask_high_words QWORD 00000ffff0000ffffh
mask_low_words QWORD 0ffff0000ffff0000h
mask_all_1 QWORD 0ffffffffffffffffh
mask_clear_word_1 QWORD 0000000000000ffffh
const_quad_735 QWORD 002df02df02df02dfh
mask_quad_green QWORD 0800080008000800h
const_quad_1500 QWORD 05dc05dc05dc05dch
DSEG ENDS
;***********************************************************************
; Constant Segment Declarations
;***********************************************************************
.const
;***********************************************************************
; Code Segment Declarations
;***********************************************************************
.code
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;; SIMD_Wood_Sqrt(u_init : DWORD, v_init : DWORD, du : DWORD, dv : DWORD,
;;;; num_pixels : DWORD)
wood_u_init = 20
wood_v_init = 24
wood_du = 28
wood_dv = 32
wood_num_pixels = 36
_SIMD_Wood_Sqrt PROC NEAR
sub esp , 16
mov [esp ], edi
mov [esp + 4], edx
mov [esp + 8], ecx
mov [esp + 12], eax
MOV ECX, wood_num_pixels[esp]
LEA EDI, _turbulenceBuf
MOVD MM4, wood_du[esp] ; 0:du
SHR ECX, 2 ; ECX= # of times to draw 4 pixels at once
MOVD MM0, wood_u_init[esp] ; 0:u
PSLLQ MM4, 32 ; du:0
PUNPCKLDQ MM0, MM0 ; u:u
MOVD MM5, wood_dv[esp] ; 0:dv
PADDD MM0, MM4 ; u + du:u
MOVD MM1, wood_v_init[esp] ; 0:v
PUNPCKHDQ MM4, MM4 ; du:du
PUNPCKLDQ MM1, MM1 ; v:v
PSLLQ MM5, 32 ; dv:0
PADDD MM1, MM5 ; v + dv:v
PUNPCKHDQ MM5, MM5 ; dv:dv
MOVQ MM2, MM0 ; u + du:u
MOVQ MM3, MM1 ; v + dv:v
PADDD MM4, MM4 ; 2du:2du
PADDD MM5, MM5 ; 2dv:2dv
PADDD MM2, MM4 ; u + 3du:u+2du
PADDD MM3, MM5 ; v + 3dv:v+2dv
PADDD MM4, MM4 ; 4du:4du
PADDD MM5, MM5 ; 4dv:4dv
MOVQ dword ptr _4du, mm4
MOVQ dword ptr _4dv, mm5
;; during the loop the following hold
;; mm0 = u1 : u0
;; mm2 = u3 : u2
;; mm1 = v1 : v0
;; mm3 = v3 : v2
;; _4du = 4du : 4du
;; _4dv = 4dv : 4dv
wood_loop:
MOVQ MM5, MM1 ; v1 : v0
MOVQ MM4, MM0 ; u1 : u0
MOVQ MM6, MM3 ; v3 : v2
PSLLD MM5, 2 ; shift left by 2 (16 -14)
MOVQ MM7, MM2 ; u3 : u2
PSRLD MM4, 14 ; shift right by 14
PAND MM5, dword ptr mask_low_words ; mm5 = v1: 0 : v0 : 0
PSLLD MM6, 2 ; shift left by 2 (16 -14)
PADDD MM0, dword ptr _4du ; u1 + 4du : u0 + 4du
POR MM4, MM5 ; mm4 = v1:u1:v0:u0
PAND MM6, dword ptr mask_low_words
PSRLD MM7, 14 ; shift left by 14
PMADDWD MM4, MM4 ; res1 = (u1*u1 + v1*v1) : res0 = (u0*u0 + v0*v0)
POR MM7, MM6 ; mm7 = v3:u3:v2:u2
PADDD MM1, dword ptr _4dv ; v1 + 4dv : v0 + 4dv
PMADDWD MM7, MM7 ; res1 = (u3*u3 + v3*v3) : res0 = (u2*u2 + v2*v2)
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;; pack the four r^2 values to words (take the results
;;;;;;;; after 10 bits shift right .
;;;;;;;; shift left by 16 , and then shift right Arithmetic by 16.
;;;;;;;;; the 16 bits shift left is done by 6 bits shift left
;;;;;;;;; instead of 10 bits shift right.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
PADDD MM2, dword ptr _4du ; u3 + 4du : u2 + 4du
PSLLD MM4, 6 ; shift left by 6 (16 -10)
PADDD MM3, dword ptr _4dv ; v3 + 4dv : v2 + 4dv
PSRAD MM4, 16 ; extend sign bit for PACKSSDW
MOVQ MM5, [EDI] ; turbulence
PSLLD MM7, 6 ; shift left by 6 (16 -10)
PMULLW MM5, dword ptr const_quad_15 ; turb = 15 * turb
PSRAD MM7, 16 ; extend sign bit for PACKSSDW
MOVQ MM6, dword ptr const_FFFF_Minus_High_sqrt
;;;;;; finally pack them correctly
;;;;;;; mm4 = ( res3:res2:res1:res0) >> 10 and packed
PACKSSDW MM4, MM7
;;; clip the values against the range [0 : 7FFh ]
;;; which is the size of the sqrt table (2048 entries)
PADDUSW MM4, MM6 ; mm6 = const_FFFF_Minus_High_sqrt
PSUBUSW MM4, MM6 ; mm6 = const_FFFF_Minus_High_sqrt
PAND MM4, dword ptr mask_odd_indexes
MOVD EAX, MM4
MOV EDX, EAX
AND EAX, 0ffffh ; eax = res0
SHR EDX, 16 ; edx = res1
PSRLQ MM4, 32
MOVD MM7, [ _sqrtTable + eax*2] ; read from the sqrt table
PUNPCKLWD MM7, [ _sqrtTable + edx*2] ; 0:0:sqrt(res1):sqrt(res0)
MOVD EAX, MM4
MOV EDX, EAX
AND EAX, 0ffffh ; eax = res2
SHR EDX, 16 ; edx = res3
MOVD MM6, [ _sqrtTable + eax*2] ; read from the sqrt table
PUNPCKLWD MM6, [ _sqrtTable + edx*2] ; 0:0:sqrt(res3):sqrt(res2)
PUNPCKLDQ MM7, MM6 ; sqrt(res3):sqrt(res2):sqrt(res1):sqrt(res0)
;;;;; mm7 = 10 * (sqrt(res3):sqrt(res2):sqrt(res1):sqrt(res0))
PMULLW MM7, dword ptr const_quad_10
ADD EDI, 8
;;;;; wood_indx = 10 * sqrt(res) + 15 * turbulence
MOVQ MM6, dword ptr const_FFFF_Minus_High_Wood
PADDW MM7, MM5
PSRLW MM7, 2 ; wood_indx >>= 2
;;; clip the values against the range [0 : 176Fh ]
;;; which is the size of the wood table (6000 entries).
PADDUSW MM7, MM6 ; mm6 = const_FFFF_Minus_High_Wood
PSUBUSW MM7, MM6 ; mm6 = const_FFFF_Minus_High_Wood
PAND MM7, dword ptr mask_odd_indexes
MOVD EAX, MM7 ; indx1:indx0
MOV EDX, EAX
AND EAX, 0ffffh ; eax = indx0
SHR EDX, 16 ; edx = indx1
MOVD MM6, [ _woodTable + eax*2] ; read wood colors from table
PSRLQ MM7, 32
PUNPCKLWD MM6, [ _woodTable + edx*2] ; 0:0:wood1:wood0
MOVD EAX, MM7 ; indx1:indx0
MOV EDX, EAX
AND EAX, 0ffffh ; eax = indx2
SHR EDX, 16 ; edx = indx3
MOVD MM7, [ _woodTable + eax*2] ; read wood colors from table
PUNPCKLWD MM7, [ _woodTable + edx*2] ; 0:0:wood3:wood2
PUNPCKLDQ MM6, MM7 ; wood3:wood2:wood1:wood0
MOVQ [EDI-8], MM6 ; store the colors into turb_buffer
DEC ECX
JNZ wood_loop
EMMS ; Clear out the MMX registers and set appropriate flags.
MOV EAX, [ESP + 12]
MOV ECX, [ESP + 8]
MOV EDX, [ESP + 4]
MOV EDI, [ESP ]
ADD ESP, 16
RET ; end of function
_SIMD_Wood_Sqrt ENDP
Appendix C - Marble Code Listing
TITLE Marble textures using MMX(TM) technology ;prevent listing of iammx.inc file .nolist INCLUDE iammx.inc .list .586 .model FLAT KLAM equ 0 ;*********************************************************************** ; Data Segment Declarations ;*********************************************************************** ;.DATA DSEG SEGMENT PARA extrn _marbleTable : ptr sword extrn _woodTable : ptr sword extrn _sqrtTable : ptr sword extrn _turbulenceBuf : ptr sword ;Variables, u, v, du, dv each contain parameters for two ;texels. Since u, v, ... are 64 bit, then each texel parameter is ;32 bit. (32 bit per texel * two texels = 64 bits). This enables us ;to work with two pixels at one time using MMX technology. ALIGN 8 _4du QWORD ? _4dv QWORD ? result dd 0 ;Various masks. Set up to filter out unwanted bits in MMX registers. ALIGN 8 const_quad_10 QWORD 000a000a000a000ah const_quad_15 QWORD 000f000f000f000fh const_FFFF_Minus_High_sqrt QWORD 0f800f800f800f800h const_FFFF_Minus_High_Wood QWORD 0e890e890e890e890h mask_odd_indexes QWORD 0fffefffefffefffeh mask_high_words QWORD 00000ffff0000ffffh mask_low_words QWORD 0ffff0000ffff0000h mask_all_1 QWORD 0ffffffffffffffffh mask_clear_word_1 QWORD 0000000000000ffffh const_quad_735 QWORD 002df02df02df02dfh mask_quad_green QWORD 0800080008000800h const_quad_1500 QWORD 05dc05dc05dc05dch DSEG ENDS ;*********************************************************************** ; Constant Segment Declarations ;*********************************************************************** .const ;*********************************************************************** ; Code Segment Declarations ;*********************************************************************** .code ;*********************************************************************** ;;;; SIMD_Marble uses the contents of _turbulenceBuf which was filled ;;;; before by SIMD_Octave with num_octaves of perlin noise. ;;;; The marble approximation is ;;;; marb(u,v) = sin(u + turb(u,v)), we use a pre-computed ;;;; sine table to accelerate it this also enables the usage of MMX technolgy ;;;; The table '_marbleTable' actually hold the marble value itself ;;;; which is a manipulation of the sine output. ;;;; In each iteration 4 pixels are calculated, 'num_pixels' is a multiply of 4. ;*********************************************************************** ;;; SIMD_Marble(u_init:DWORD, du:DWORD, num_pixels:DWORD ) marb_u_init = 20 marb_du = 24 marb_num_pixels = 28 _SIMD_Marble PROC NEAR SUB ESP, 16 MOV [ESP + 12], EAX MOV [ESP + 8], ECX MOV [ESP + 4], EBX MOV [ESP ], EDI MOV ECX, marb_num_pixels[esp] ; number of pixels in scanline LEA EDI, _turbulenceBuf ; already calculated turbulence MOVD MM2, marb_du[esp] ; mm2 = 0:du MOVD MM0, marb_u_init[esp] ; mm0 = 0: PSLLQ MM2, 32 ; mm2 = du:0 SHR ECX, 2 ; ecx = # of times to draw 4 pixels at once PUNPCKLDQ MM0, MM0 ; u : u PADDD MM0, MM2 ; u + du : u PUNPCKHDQ MM2, MM2 ; du : du MOVQ MM1, MM0 ; u + du : u PADDD MM2, MM2 ; 2du : 2du PADDD MM1, MM2 ; u + 3du : u + 2du PADDD MM2, MM2 ; 4du : 4du if (KLAM) MOVQ MM6, dword ptr const_quad_10 endif ;; during the loop the following hold ;; mm0 = u1 : u0 ;; mm1 = u3 : u2 ;; mm2 = 4du: 4du ;; if KLAM is defined then ;; mm6 = 10:10:10:10 ;; on P55C it is paired on the u pipe ;; so we can PAND with memory marb_loop: MOVQ MM5, [EDI] ; mm5 = turb3:turb2:turb1:turb0 MOVQ MM3, MM0 ; mm3 = u1:u0 MOVQ MM4, MM1 ; mm4 = u3:u2 ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;; the following lines pack u3,u2,u1,u0 from two registers ;;;; to one register including shift right by 14 . ;;;; in order to make packssdw not to change the numbers ;;;; but only pack them we do shift left by 16 and then ;;;; shift right arithmetic by 16 to extend the sign bit . ;;;; The 16 bits shift left is done by 2 bits shift left ;;;;; instead of 14 bits shift right. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; PSLLD MM3, 2 ; shift left by 2 (16 -14) if ( KLAM ) PMULLW MM5, MM6 ; turb = 10 * turb else PMULLW MM5, dword ptr const_quad_10 ; turb = 10 * turb endif PSLLD MM4, 2 ; shift left by 2 (16 -14) PADDD MM0, MM2 ; increment each of u1:u0 by 4du for next iteration PSRAD MM3,16 ; extend sign bit for PACKSSDW PSRAD MM4,16 ; extend sign bit for PACKSSDW ADD EDI,8 ; increment edi for next iteration PACKSSDW MM3, MM4 ; mm3 = (u3:u2:u1:u0) >> 14 and packed PADDD MM1, MM2 ; increment each of u3:u2 by 4du for next iteration PADDW MM3, MM5 ; marble indexes are: (u_init >> 14) + (10 * turb) ;;;;; now read the colors from the marble table ;;;;; the input to this part is mm3 = indx3:indx2:indx1:indx0 ;;;;; the output is mem[edi-8] = pixel3 :pixel2 :pixel1 :pixel0 PAND MM3, dword ptr mask_odd_indexes MOVD EAX, MM3 ; eax = indx1:indx0 MOV EBX, EAX ; ebx = indx1:index0 AND EAX, 0ffffh ; eax = indx0 SHR EBX, 16 ; edx = indx1 PSRLQ MM3, 32 ; mm3 = 0:0:indx3:indx2 MOVD MM4, [ _marbleTable + eax*2] ; read from the marble table PUNPCKLWD MM4, [ _marbleTable + ebx*2] ; 0:0:marb1:marb0 MOVD EAX, MM3 ; eax = indx3:indx2 MOV EBX, EAX ; ebx = indx3:index2 AND EAX, 0ffffh ; eax = indx2 SHR EBX, 16 ; edx = indx3 MOVD MM5, [ _marbleTable + eax*2] ; read from the marble table PUNPCKLWD MM5, [ _marbleTable + ebx*2] ; 0:0:marb3:marb2 PUNPCKLDQ MM4, MM5 ; marb3:marb2:marb1:marb0 MOVQ [EDI-8], MM4 ; store the 4 pixels to turb_buffer DEC ECX JNZ marb_loop EMMS ; Clear out the MMX registers and set appropriate flags. MOV EAX, [ESP + 12] MOV ECX, [ESP + 8] MOV EBX, [ESP + 4] MOV EDI, [ESP ] ADD ESP, 16 RET ; end of function _SIMD_Marble ENDP
Appendix D - DDU and DDV Code Listing
;Get the UV parameters in MMX(TM) technology form. ;Note: UV texel values are stored in 10.22 fixed integer format. ;This sets up the U parameters for pixels 1 and 3 in MM0 register and ;V parameter in MM1 register. After setup, the registers will contain: ; |--------- 32 bit ------------| ; +-------------------------------------------------------------------+ ;MM0 = | U texel for pix #1 = u + du | U texel for pix #3 = u + 3du + 3ddu | ; +-------------------------------------------------------------------+ ; +-------------------------------------------------------------------+ ;MM1 = | V texel for pix #1 = v + dv | V texel for pix #3 = v + 3dv + 3ddv | ; +-------------------------------------------------------------------+ ;This is because the first four pixels drawn on the screen will have the ;U and V texel values of: ;Pixel #0 = u ;Pixel #1 = u + du ;Pixel #2 = u + 2du + ddu ;Pixel #3 = u + 3du + 3ddu ;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged. MOVD MM0, u_init SHR ECX, 2 ;ECX= # of times to draw 4 pixels at once MOVD MM1, v_init PUNPCKLDQ MM0, MM0 ;U p1 = u, p3 = u MOVD MM2, du_init PUNPCKLDQ MM1, MM1 ;V p1 = v, p3 = v MOVD MM3, dv_init PADDD MM0, MM2 ;U p1 = u, p3 = u + du PADDD MM1, MM3 ;V p1 = v, p3 = v + dv PADDD MM0, MM2 ;U p1 = u, p3 = u + 2du PADDD MM1, MM3 ;V p1 = v, p3 = v + 2dv PUNPCKLDQ MM2, MM2 PUNPCKLDQ MM3, MM3 PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du MOVD MM2, ddu_init PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv MOVD MM3, ddv_init PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du + ddu PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv + ddv PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du + 2ddu PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv + 2ddv PADDD MM0, MM2 ;U p1 = u + du, p3 = u + 3du + 3ddu MOVQ DWORD PTR u, MM0 PADDD MM1, MM3 ;V p1 = v + dv, p3 = v + 3dv + 3ddv MOVQ DWORD PTR v, MM1 ;Get the du dv parameters in MMX(TM) technology form ;Note: du dv texel values are stored in 10.22 fixed integer format. ;This sets up the du parameters for pixels 1 and 3 in MM0 register and ;dv parameter in MM1 register. After setup, the registers will contain: ; |--------- 32 bit --------------| ; +---------------------------------------------------------------+ ;MM0 = | DU texel for p1 = 4du + 10ddu | DU texel for p3 = 4du + 18ddu | ; +---------------------------------------------------------------+ ; +---------------------------------------------------------------+ ;MM1 = | DV texel for p1 = 4dv + 10ddv | DV texel for p3 = 4dv + 18ddv | ; +---------------------------------------------------------------+ ;This is because after the first four pixels are drawn on the screen, the ;loop repeats to draw the next four pixels. In order to get the next u, v ;texel coordinates, appropriate du, dv values need to be summed to u and v. ;The correct starting values of du and dv are: ;Pixel #0 = 4du + 6ddu ;Note: these have been mathematically proven. ;Pixel #1 = 4du + 10ddu ;Pixel #2 = 4du + 14ddu ;Pixel #3 = 4du + 18ddu ;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged. MOVD MM0, du_init ;DU p1 = 0, p3 = du MOVD MM1, dv_init ;DV p1 = 0, p3 = dv PUNPCKLDQ MM0, MM0 ;DU p1 = du, p3 = du PUNPCKLDQ MM1, MM1 ;DV p1 = dv, p3 = dv MOVD MM2, ddu_init PSLLD MM0, 2 ;DU p1 = 4du, p3 = 4du MOVD MM3, ddv_init PSLLD MM1, 2 ;DV p1 = 4dv, p3 = 4dv PUNPCKLDQ MM2, MM2 PUNPCKLDQ MM3, MM3 PSLLD MM2, 1 PSLLD MM3, 1 PADDD MM0, MM2 ;DU p1 = 4du + 2ddu, p3 = 4du + 2ddu PADDD MM1, MM3 ;DV p1 = 4dv + 2ddv, p3 = 4dv + 2ddv PSLLD MM2, 2 PSLLD MM3, 2 PADDD MM0, MM2 ;DU p1 = 4du + 10ddu, p3 = 4du + 10ddu MOVD MM2, ddu_init ;DDU p1 = 0, p3 = ddu PADDD MM1, MM3 ;DV p1 = 4dv + 10ddv, p3 = 4dv + 10ddv MOVD MM3, ddv_init ;DDV p1 = 0, p3 = ddv PSLLD MM2, 3 ;DDU p1 = 0, p3 = 8ddu PSLLD MM3, 3 ;DDV p1 = 0, p3 = 8ddv PADDD MM0, MM2 ;DU p1 = 4du + 10ddu, p3 = 4du + 18ddu PADDD MM1, MM3 ;DV p1 = 4dv + 10ddv, p3 = 4du + 18ddv PSLLD MM2, 1 ;DDU p1 = 0, p3 = 16ddu MOVQ DWORD PTR du, MM0 PUNPCKLDQ MM2, MM2 ;DDU p1 = 16ddu, p3 = 16ddu MOVQ DWORD PTR dv, MM1 ;Get the ddu ddv parameters in MMX(TM) technology form ;Note: ddu ddv texel values are stored in 10.22 fixed integer format. ;This sets up the ddu parameters for pixels 1 and 3 in MM0 register and ;ddv parameter in MM1 register. After setup, the registers will contain: ; |--------- 32 bit ---------| ; +-----------------------------------------------------+ ;MM0 = | DDU texel for p1 = 16ddu | DDU texel for p3 = 16ddu | ; +-----------------------------------------------------+ ; +-----------------------------------------------------+ ;MM1 = | DDV texel for p1 = 16ddv | DDV texel for p3 = 16ddv | ; +-----------------------------------------------------+ ;This is because after the first four pixels are drawn on the screen, the ;loop repeats to draw the next four pixels. In order to get the next du, dv ;texel coordinates, appropriate ddu, ddv values need to be summed to du and dv. ;The correct values of ddu and ddv are: ;Pixel #0 = 16ddu ;Note: these have been mathematically proven. ;Pixel #1 = 16ddu ;Pixel #2 = 16ddu ;Pixel #3 = 16ddu ;We are only interested in pixels #1 and #3 because pixels #0 and #2 are averaged. PSLLD MM3, 1 ;DDV p1 = 0, p3 = 16ddv MOVQ DWORD PTR ddu, MM2 PUNPCKLDQ MM3, MM3 ;DDV p1 = 16ddv, p3 = 16ddv MOVQ DWORD PTR ddv, MM3
Appendix E - Z-Buffer Scanline Algorithm
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;; z is calculated along the scan line z = z_init + i * dz_init
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
MMX_INCZbuffer PROC NEAR C USES edi esi ecx eax ebx,
z_init: DWORD, dz_init: DWORD,
num_pixels: DWORD, z_line: PTR SWORD, color_line: PTR SWORD,
z_buffer: PTR SWORD, color_buffer: PTR SWORD
MOVD MM1, dz_init
MOVD MM4, z_init
MOVD MM5, dz_init
PSLLD MM1, 16 ;0:0:dz:0
PAND MM4, DWORD PTR mask_clear_byte_1
MOVQ MM6, DWORD PTR mask_all_1
PUNPCKLWD MM4, MM4 ;0:0:z:z
PADDSW MM4, MM1 ;0:0:z + dz:z
PUNPCKLWD MM5, MM5 ;0:0:dz:dz
MOVQ MM3, MM4 ;0:0:z + dz:z
PSLLW MM5, 1 ;0:0:2dz:2dz
PSLLQ MM3, 32 ;z + dz:z:0:0
MOV EAX, z_buffer
PSLLQ MM5, 32 ;2dz:2dz:0:0
MOV EDI, color_line
PADDSW MM3, MM5 ;z+3z:z+2dz:0:0
PUNPCKHDQ MM5, MM5 ;2dz:2dz:2dz:2dz
POR MM4, MM3 ;z+3z:z+2dz:z + dz:z
PSLLW MM5, 1 ;4dz:4dz:4dz:4dz
MOV ECX, color_buffer
MOV ESI, num_pixels
SHR ESI, 2
zLoop:
MOVQ MM0, [eax] ;mm0 = Za,Za,Za,Za (load)
MOVQ MM1, MM4 ;[ebx] mm1 = Zb,Zb,Zb,Zb (load)
MOVQ MM2, MM0 ;mm2 = Za,Za,Za,Za (will be the mask)
PADDSW MM4, MM5
PCMPGTW MM2, MM1 ;mm2 = mask of 0000 or fffff (4 times)
ADD EAX, 8
MOVQ MM3, MM2 ;(after pxor) mm3 = ~mm2 (mm2 xor fffffffffffffff)
PAND MM1, MM2 ;mm1 = only the Zb's which are less then the Za's
PXOR MM3, MM6 ;DWORD PTR mask_all_1
ADD ECX, 8
PAND MM0, MM3 ;mm0 = the Za's which are less or EQUAL the Zb's
ADD EDI, 8
POR MM0, MM1 ;mm0 = the wanted Z's
MOVQ [eax-8], MM0 ;(store Z's)
MOVQ MM0, [ecx-8] ;mm0 = Ca,Ca,Ca,Ca
MOVQ MM1, [edi-8] ;mm1 = Cb,Cb,Cb,Cb
PAND MM1, MM2 ;mm1 = the Ca's of the 'Good' Za's
PAND MM0, MM3 ;mm0 = the Cb's of the 'Good' Zb's
POR MM0, MM1 ;the wanted C's
MOVQ [edi-8], MM0 ;(store)
DEC ESI
JNZ zLoop
EMMS
RET
MMX_INCZbuffer ENDP
; Note, registers ESI, EDI, MM1, MM2, MM3, MM4, MM6, MM7 are modified by this routine. MOVQ MM4, low_z ;Move two rightmost Z-Buffer values into MM4 (LSD) MOVQ MM2, high_z ;Move the leftmost Z-Buffer values into MM2 (MSD) MOVQ MM6, MM4 ;Make a copy of LSD of the Z-Buffer values MOVQ MM7, z_inc ;Move the Z-incremental into a register for future use. PSRAD MM4, 16 ;Discard the fractional part of the two Z values PUSH ESI ;Save ESI PSRAD MM2, 16 ;Discard the fractional part of the two Z values MOV ESI, z_buffer ;ESI = pointer to four Z values being looked at in Z-Buffer. PACKSSDW MM4, MM2 ;Mesh all four Z-Buffer values into one register MOVQ MM2, [ESI] ;MM2 = the old Z values currently in the Z-Buffer. PADDD MM6, MM7 ;Add DZ to Z MOVQ MM7, high_z ;Save a copy of high_z PCMPGTW MM2, MM4 ;Perform a compare between the old and the new Z values. PADDD MM7, z_inc ;Add DZ to Z MOVQ MM3, MM2 ;Save a copy of the compare results PANDN MM3, [EDI] ;MM3 = Colors of previous pixels to be drawn. PAND MM1, MM2 ;MM1 = Colors of current pixel 4 pixels to be drawn. MOVQ high_z, MM7 ;Update the high_z variable POR MM1, MM3 ;"OR" old and new contents together for the 4 pixel colors. MOVQ low_z, MM6 ;Update the low_z variable MOVQ MM3, MM2 ;Save a copy of the compare results PANDN MM3, [ESI] ;[ESI] = Pointer to existing 4 Z-Buffer values. PAND MM2, MM4 MOVQ [EDI], MM1 ;Write out the 4 pixels to video memory. POR MM2, MM3 ;"OR" old and new contents together for the 4 Z values. MOVQ [ESI], MM2 ;Update the Z-Buffer with the 4 new values. ADD z_buffer, 8 ;z_buffer pointer is incremented eight bytes (4 pixels). POP ESI ;Restore ESI
;***********************************************************************
;;; This is the wood implementation by linear curves in the u_v plane.
;;;; In each iteration 4 pixels are calculated, 'num_pixels' is a multiply of 4.
;***********************************************************************
;;;; SIMD_Wood_Linear(u_init: DWORD, v_init: DWORD, du: DWORD, dv : DWORD, num_pixels:DWORD)
_SIMD_Wood_Linear PROC NEAR
SUB ESP, 16
MOV [ESP + 12], EAX
MOV [ESP + 8], ECX
MOV [ESP + 4], EDX
MOV [ESP ], EDI
MOV ECX, wood_num_pixels[esp]
MOVD MM4, wood_du[esp] ; 0:du
SHR ECX, 2 ; ECX= # of times to draw 4 pixels at once
LEA EDI, _turbulenceBuf
MOVD MM0, wood_u_init[esp] ; 0:u
PSLLQ MM4, 32 ; du:0
PUNPCKLDQ MM0, MM0 ; u:u
MOVD MM5, wood_dv[esp] ; 0:dv
PADDD MM0, MM4 ; u + du:u
MOVD MM1, wood_v_init[esp] ; 0:v
PUNPCKHDQ MM4, MM4 ; du:du
PUNPCKLDQ MM1, MM1 ; v:v
PSLLQ MM5, 32 ; dv:0
PADDD MM1, MM5 ; v + dv:v
PUNPCKHDQ MM5, MM5 ; dv:dv
MOVQ MM2, MM0 ; u + du:u
MOVQ MM3, MM1 ; v + dv:v
PADDD MM4, MM4 ; 2du:2du
PADDD MM5, MM5 ; 2dv:2dv
PADDD MM2, MM4 ; u + 3du:u+2du
PADDD MM3, MM5 ; v + 3dv:v+2dv
PADDD MM4, MM4 ; 4du:4du
PADDD MM5, MM5 ; 4dv:4dv
MOVQ dword ptr _4dv, MM5
;; during the loop the following hold
;; mm0 = u1 : u0
;; mm2 = u3 : u2
;; mm1 = v1 : v0
;; mm3 = v3 : v2
;; mm4 = 4du : 4du
;; _4dv = 4dv : 4dv
wood_loop:
MOVQ MM5, MM0 ; u1 : u0
MOVQ MM6, MM2 ; u3 : u2
;; like in the marble code, in order to shift right by 14
;; and then pack 4 dwords to 4 words in one MMX(TM) register
;; a shift left followed by shift right arithmetic are done
;;; as in the marble the shift left is by 2 .
PADDD MM0, MM4 ; u1 + 4du : u0 + 4du
PSLLD MM5, 2 ; shift left by 2 (16 -14)
PADDD MM2, MM4 ; u3 + 4du : u2 + 4du
PSLLD MM6, 2 ; shift left by 2 (16 -14)
MOVQ MM7, MM1 ; v1 : v0
PSRAD MM5, 16 ; extend sign bit for PACKSSDW
PADDD MM1, dword ptr _4dv ; v1 + 4dv : v0 + 4dv
PSRAD MM6, 16 ; extend sign bit for PACKSSDW
;;;;;;;; finally pack them correctly
;;;;;;;; mm5 = (u3:u2:u1:u0) >> 14 and packed
PACKSSDW MM5, MM6
MOVQ MM6, MM3 ; v3 : v2
PSLLD MM7, 2 ; shift left by 2 (16 -14)
PADDD MM3, dword ptr _4dv ; v3 + 4dv : v2 + 4dv
PSLLD MM6, 2 ; shift left by 2 (16 -14)
PSRAD MM6, 16 ; extend sign bit for PACKSSDW
PSRAD MM7, 16 ; extend sign bit for PACKSSDW
;;;;;;;; mm7 = (v3:v2:v1:v0) >> 14 and packed
PACKSSDW MM7, MM6
MOVQ MM6, MM5 ; the following instructions implement
; Unsigned absolute value for words
PSUBUSW MM5, MM7
PSUBUSW MM7, MM6
MOVQ MM6, [EDI] ; turbulence
POR MM5, MM7 ; mm5 = abs(v3 - u3 : v2 - u2 : v1 - u1 : v0 - u0)
;;;;;; wood_indx = (10 * abs(u-v) + 15 * turbulence(u,v) ) >> 2
PMULLW MM6, dword ptr const_quad_15 ; turb = 15 * turb
PMULLW MM5, dword ptr const_quad_10 ; | u - v | * 10
MOVQ MM7, dword ptr const_FFFF_Minus_High_Wood
PADDW MM5, MM6 ; 10 * abs | u - v | + 15 * turb(u,v)
ADD EDI, 8
PSRLW MM5, 2 ; wood_indx >>= 2
;;; Now clip the values against the range [0 : 176Fh ]
;;; which is the size of the wood table (6000 entries).
;;; paddusw saturates each value above 176FH to FFFF
;;; psubusw undo the offset
PADDUSW MM5, MM7 ; mm7 = const_FFFF_Minus_High_Wood
PSUBUSW MM5, MM7 ; mm7 = const_FFFF_Minus_High_Wood
;;;; on P55C each unaligned load of 4 bytes (movd) cause penalty
;;;; so we don't read odd indexes (the table's element size is word )
PAND MM5, dword ptr mask_odd_indexes
MOVD EAX, MM5 ; eax= indx1:indx0
MOV EDX, EAX ; edx = indx1:indx0
AND EAX, 0ffffh ; eax = indx0
SHR EDX, 16 ; edx = indx1
PSRLQ MM5, 32 ; mm5 = indx3:indx2
MOVD MM6, [ _woodTable + eax*2] ; read wood colors from table
PUNPCKLWD MM6, [ _woodTable + edx*2] ; 0:0:wood1:wood0
MOVD EAX, MM5 ; eax = indx3:indx2
MOV EDX, EAX ; edx = indx3:indx2
AND EAX, 0ffffh ; eax = indx2
SHR EDX, 16 ; edx = indx3
MOVD MM5, [ _woodTable + eax*2] ; read wood colors from table
PUNPCKLWD MM5, [ _woodTable + edx*2] ; 0:0:wood3:wood2
PUNPCKLDQ MM6, MM5 ; mm6 = wood3:wood2:wood1:wood0
MOVQ [EDI-8], MM6 ; store the colors into turb_buffer
DEC ECX
JNZ wood_loop
EMMS ; Clear out the MMX registers and set appropriate flags.
MOV EAX, [ESP + 12]
MOV ECX, [ESP + 8]
MOV EDX, [ESP + 4]
MOV EDI, [ESP ]
ADD ESP, 16
RET ; end of function
_SIMD_Wood_Linear ENDP
* Legal Information © 1998 Intel Corporation